
Тригонометрическая таблица sin cos tan представляет собой серию таблиц, содержащих тригонометрическое значение или тангенс угла sin cos.
В этой статье таблица тригонометрических значений sin cos tan показана под различными особыми углами от угла 0º до 360º (или того, что обычно называется углом круга 360 градусов), так что вам больше не придется запоминать их.
Что касается формулы тригонометрического тождества, вы можете прочитать ее в этой статье.
Определение Sin Cos Tan
Прежде чем вводить таблицу тригонометрических значений, рекомендуется сначала понять термины тригонометрия и sin cos tan.
- Тригонометрия - это раздел математики, изучающий взаимосвязь между длиной и углом треугольника.
- Sin (синус) - это отношение длины треугольника между передней частью угла и гипотенузой y / z.
- Cos (косинус) - это отношение длины в треугольнике между стороной угла и гипотенузой, x / z.
- Тан (тангенс) - это отношение длин треугольника между передней частью угла и стороной y / x.

Все тригонометрические сравнения tan sin cos ограничиваются только допустимыми прямоугольными треугольниками или треугольниками с одним углом 90 градусов.
Таблица тригонометрии со специальным углом в квадранте I (0 - 90 градусов)
| Угловой | 0 º | 30 º | 45 º | 60 º | 90 º |
| Грех | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Загар | 0 | 1/2 √3 | 1 | √3 | ∞ |
Специальный угловой квадрант II (90 - 180 градусов) Таблица тригонометрии
| Угловой | 90 º | 120 º | 135 º | 150 º | 180 º |
| Грех | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Cos | 0 | - 1/2 | - 1/2 √2 | - 1/2 √3 | -1 |
| Загар | ∞ | -√3 | -1 | - 1/3 √3 | 0 |
Sin Cos Tan Table Special Angle Quadrant III (180 - 270 градусов)
| Угловой | 180 º | 210 º | 225 º | 240 º | 270 º |
| Грех | 0 | - 1/2 | - 1/2 √2 | - 1 / 2√3 | -1 |
| Cos | -1 | - 1 / 2√3 | - 1 / 2√2 | - 1/2 | 0 |
| Загар | 0 | 1 / 3√3 | 1 | √3 | ∞ |
Специальный угловой квадрант IV стола Cos Sin Tan (270 - 360 градусов)
| Угловой | 270 º | 300 º | 315 º | 330 º | 360 º |
| Грех | -1 | -½√3 | -½√2 | -½ | 0 |
| Cos | 0 | ½ | ½√2 | ½√3 | 1 |
| Загар | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
Это полный список тригонометрических таблиц для всех специальных углов от 0 до 360 градусов.
Также прочтите: Процесс работы с механизмами зрения человека и советы по уходу за глазамиВы можете использовать эти таблицы, чтобы упростить бизнес при вычислении или анализе тригонометрии в математике.
Вызов тригонометрической таблицы со специальным углом без запоминания
Фактически, вам не нужно запоминать все тригонометрические значения со всех сторон.
Все, что вам нужно, это базовая концепция понимания, которую вы можете использовать, чтобы найти значение триггера для любого конкретного угла.
Вам просто нужно запомнить компоненты длины стороны треугольника под особыми углами 0, 30, 45, 60 и 90 градусов.
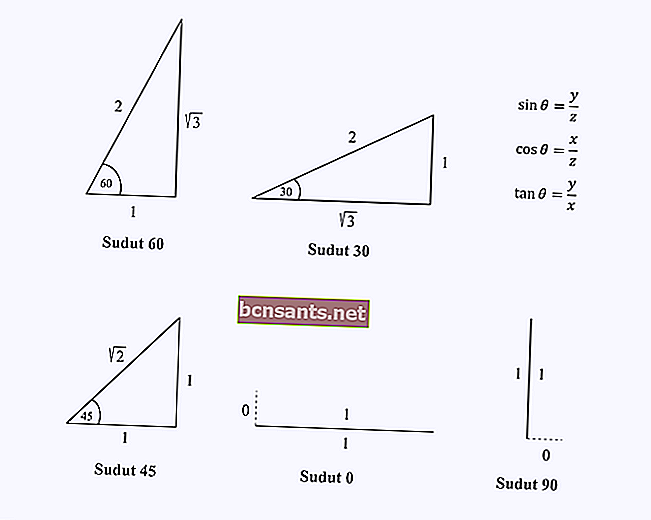
Предположим, вы хотите найти значение cos (60).
Вам нужно только запомнить длину стороны треугольника с углом 60 градусов, а затем выполнить операцию косинуса, которая равна x / z на этом треугольнике.
Из рисунка видно, что значение cos 60 = 1/2.
Легко, правда?
Для углов в других квадрантах метод тот же, и вам нужно только настроить положительный или отрицательный знак для каждого квадранта.
Таблица в форме круга
Если приведенная выше таблица cos sin tan слишком длинна для запоминания, а также если метод концепции специального угла, по вашему мнению, все еще труден ...
Вы можете использовать тригонометрическую таблицу в форме круга, чтобы непосредственно увидеть значение sin cos tan под углом в 360 градусов.
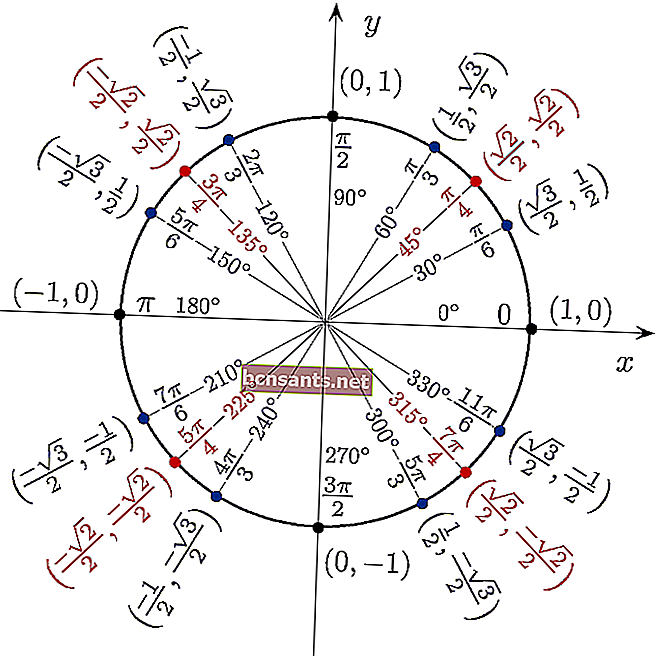
Быстрые приемы запоминания тригонометрических таблиц
В дополнение к описанным выше методам есть еще один метод, который вы можете использовать, чтобы легко запомнить таблицы тригонометрических формул.
Вам нужно сделать следующие шаги:
- Шаг 1 . Создайте таблицу, содержащую углы от 0 до 90 градусов и столбцы с описанием sin cos tan
- Шаг 2 . Обратите внимание, что общая формула для sin в диапазоне от 0 до 90 градусов равна √x / 2.
- Шаг 3 . Измените значение x на 0 на √x / 2 в самом первом столбце. Верхний левый угол.
- Шаг 4. Заполните последовательность, изменив x на 0, 1, 2, 3, 4 в столбце sin. Таким образом, вы получили полное тригонометрическое значение sin
- Шаг 5 . Чтобы найти значение cos, все, что вам нужно сделать, это изменить порядок в столбце sin.
- Шаг 6 . Чтобы найти значение tan, все, что вам нужно сделать, это разделить значение sin на значение cos.
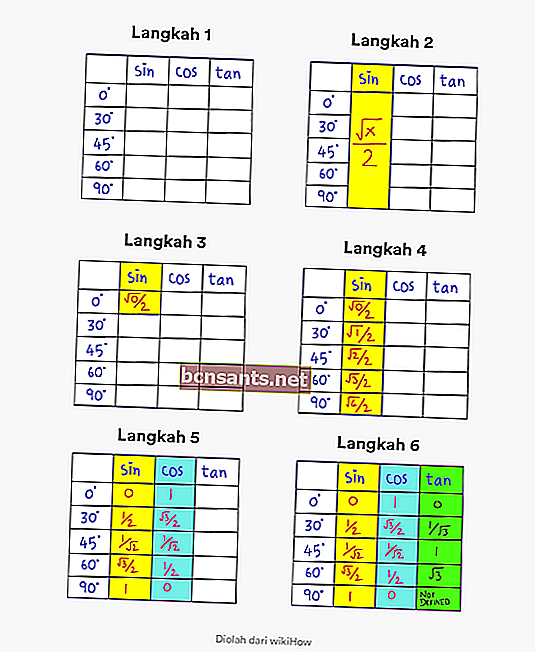
Какой из них вам легче понять, чтобы запомнить триггерное значение tan sin cos?
В любом случае выберите тот, который вам легче всего понять. Потому что у каждого человека свой стиль обучения.
Таблицы для всех углов
Если в таблицах выше показаны только тригонометрические значения особых углов, то в этой таблице показаны все тригонометрические значения всех углов от 0 до 90 градусов.
| Угловой | Радианы | Грех | Cos | Загар |
| 0 ° | 0 | 0 | 1 | 0 |
| 1 ° | 0,01746 | 0,01746 | 0,99985 | 0,01746 |
| 2 ° | 0,03492 | 0,03491 | 0,99939 | 0,03494 |
| 3 ° | 0,05238 | 0,05236 | 0,99863 | 0,05243 |
| 4 ° | 0,06984 | 0,06979 | 0,99756 | 0,06996 |
| 5 ° | 0,0873 | 0,08719 | 0,99619 | 0,08752 |
| 6 ° | 0,10476 | 0,10457 | 0,99452 | 0,10515 |
| 7 ° | 0,12222 | 0,12192 | 0,99254 | 0,12283 |
| 8 ° | 0,13968 | 0,13923 | 0,99026 | 0,1406 |
| 9 ° | 0,15714 | 0,1565 | 0,98768 | 0,15845 |
| 10 ° | 0,1746 | 0,17372 | 0,9848 | 0,1764 |
| 11 ° | 0,19206 | 0,19089 | 0,98161 | 0,19446 |
| 12 ° | 0,20952 | 0,20799 | 0,97813 | 0,21265 |
| 13 ° | 0,22698 | 0,22504 | 0,97435 | 0,23096 |
| 14 ° | 0,24444 | 0,24202 | 0,97027 | 0,24943 |
| 15 ° | 0,26191 | 0,25892 | 0,9659 | 0,26806 |
| 16 ° | 0,27937 | 0,27575 | 0,96123 | 0,28687 |
| 17 ° | 0,29683 | 0,29249 | 0,95627 | 0,30586 |
| 18 ° | 0,31429 | 0,30914 | 0,95102 | 0,32506 |
| 19 ° | 0,33175 | 0,32569 | 0,94548 | 0,34448 |
| 20 ° | 0,34921 | 0,34215 | 0,93965 | 0,36413 |
| 21 ° | 0,36667 | 0,35851 | 0,93353 | 0,38403 |
| 22 ° | 0,38413 | 0,37475 | 0,92713 | 0,40421 |
| 23 ° | 0,40159 | 0,39088 | 0,92044 | 0,42467 |
| 24 ° | 0,41905 | 0,40689 | 0,91348 | 0,44543 |
| 25 ° | 0,43651 | 0,42278 | 0,90623 | 0,46652 |
| 26 ° | 0,45397 | 0,43854 | 0,89871 | 0,48796 |
| 27 ° | 0,47143 | 0,45416 | 0,89092 | 0,50976 |
| 28 ° | 0,48889 | 0,46965 | 0,88286 | 0,53196 |
| 29 ° | 0,50635 | 0,48499 | 0,87452 | 0,55458 |
| 30 ° | 0,52381 | 0,50018 | 0,86592 | 0,57763 |
| 31 ° | 0,54127 | 0,51523 | 0,85706 | 0,60116 |
| 32 ° | 0,55873 | 0,53011 | 0,84793 | 0,62518 |
| 33 ° | 0,57619 | 0,54483 | 0,83854 | 0,64974 |
| 34 ° | 0,59365 | 0,55939 | 0,8289 | 0,67486 |
| 35 ° | 0,61111 | 0,57378 | 0,81901 | 0,70057 |
| 36 ° | 0,62857 | 0,58799 | 0,80887 | 0,72693 |
| 37 ° | 0,64603 | 0,60202 | 0,79848 | 0,75396 |
| 38 ° | 0,66349 | 0,61587 | 0,78785 | 0,78172 |
| 39 ° | 0,68095 | 0,62953 | 0,77697 | 0,81024 |
| 40 ° | 0,69841 | 0,643 | 0,76586 | 0,83958 |
| 41 ° | 0,71587 | 0,65628 | 0,75452 | 0,86979 |
| 42 ° | 0,73333 | 0,66935 | 0,74295 | 0,90094 |
| 43 ° | 0,75079 | 0,68222 | 0,73115 | 0,93308 |
| 44 ° | 0,76825 | 0,69488 | 0,71913 | 0,96629 |
| 45 ° | 0,78571 | 0,70733 | 0,70688 | 1 00063 |
| 46 ° | 0,80318 | 0,71956 | 0,69443 | 1,0362 |
| 47 ° | 0,82064 | 0,73158 | 0,68176 | 1,07308 |
| 48 ° | 0,8381 | 0,74337 | 0,66888 | 1,11137 |
| 49 ° | 0,85556 | 0,75494 | 0,6558 | 1,15117 |
| 50 ° | 0,87302 | 0,76627 | 0,64252 | 1,1926 |
| 51 ° | 0,89048 | 0,77737 | 0,62904 | 1,2358 |
| 52 ° | 0,90794 | 0,78824 | 0,61537 | 1,28091 |
| 53 ° | 0,9254 | 0,79886 | 0,60152 | 1,32807 |
| 54 ° | 0,94286 | 0,80924 | 0,58748 | 1,37748 |
| 55 ° | 0,96032 | 0,81937 | 0,57326 | 1.42932 |
| 56 ° | 0,97778 | 0,82926 | 0,55887 | 1,48382 |
| 57 ° | 0,99524 | 0,83889 | 0,5443 | 1,54122 |
| 58 ° | 1,0127 | 0,84826 | 0,52957 | 1,60179 |
| 59 ° | 1.03016 | 0,85738 | 0,51468 | 1,66584 |
| 60 ° | 1,04762 | 0,86624 | 0,49964 | 1,73374 |
| 61 ° | 1,06508 | 0,87483 | 0,48444 | 1,80587 |
| 62 ° | 1,08254 | 0,88315 | 0,46909 | 1,8827 |
| 63 ° | 1.1 | 0,89121 | 0,4536 | 1 96476 |
| 64 ° | 1,11746 | 0,89899 | 0,43797 | 2,05265 |
| 65 ° | 1,13492 | 0,9065 | 0,4222 | 2,14707 |
| 66 ° | 1,15238 | 0,91373 | 0,40631 | 2,24884 |
| 67 ° | 1,16984 | 0,92069 | 0,3903 | 2,35894 |
| 68 ° | 1,1873 | 0,92736 | 0,37416 | 2,4785 |
| 69 ° | 1,20476 | 0,93375 | 0,35792 | 2,60887 |
| 70 ° | 1,22222 | 0,93986 | 0,34156 | 2,75169 |
| 71 ° | 1,23968 | 0,94568 | 0,3251 | 2,90892 |
| 72 ° | 1,25714 | 0,95121 | 0,30854 | 3,08299 |
| 73 ° | 1,2746 | 0,95646 | 0,29188 | 3,27686 |
| 74 ° | 1,29206 | 0,96141 | 0,27514 | 3,49427 |
| 75 ° | 1,30952 | 0,96606 | 0,25831 | 3,73993 |
| 76 ° | 1,32698 | 0,97043 | 0,2414 | 4,0 1992 |
| 77 ° | 1,34444 | 0,97449 | 0,22442 | 4,34219 |
| 78 ° | 1,36191 | 0,97826 | 0,20738 | 4,71734 |
| 79 ° | 1,37937 | 0,98173 | 0,19026 | 5,15984 |
| 80 ° | 1,39683 | 0,98491 | 0,1731 | 5,68998 |
| 81 ° | 1,41429 | 0,98778 | 0,15587 | 6,33709 |
| 82 ° | 1,43175 | 0,99035 | 0,1386 | 7,14523 |
| 83 ° | 1,44921 | 0,99262 | 0,12129 | 8,18379 |
| 84 ° | 1,46667 | 0,99458 | 0,10394 | 9 56868 |
| 85 ° | 1,48413 | 0,99625 | 0,08656 | 11 5092 |
| 86 ° | 1,50159 | 0,99761 | 0,06915 | 14,4259 |
| 87 ° | 1,51905 | 0,99866 | 0,05173 | 19 3069 |
| 88 ° | 1,53651 | 0,99941 | 0,03428 | 29 153 |
| 89 ° | 1,55397 | 0,99986 | 0,01683 | 59,4189 |
| 90 ° | 1,57143 | 1 | 0 | ∞ |
Надеюсь, это тригонометрическое объяснение может быть вам полезно.
Этот материал будет очень полезен для различных приложений в продвинутой математике и физике.
Вы также можете изучить другие школьные материалы в Saintif, такие как простые числа, преобразование единиц измерения, прямоугольные формулы и т. Д.
Справка
- Тригонометрия - Википедия
- Математические инструменты - тригонометрия
