
Формула для треугольника, чтобы найти площадь формы, равна 1/2 x основание x высота, чтобы найти периметр треугольника, его можно найти, сложив длины каждой стороны треугольника.
В математике нас учат различным формам. Один из них - треугольник. Форма треугольника - это самая простая форма среди различных типов фигур.
Треугольник образован тремя сторонами с тремя углами, ограниченными отрезком. Также общий угол треугольника составляет 180 градусов.
Есть несколько типов треугольников. В зависимости от длины сторон бывают равносторонние треугольники с равной длиной сторон, равнобедренные треугольники с двумя равными сторонами ног и любой треугольник с разной длиной трех сторон.
Между тем, исходя из угла, существует острый треугольник с углом менее 90 градусов, тупой треугольник с одним углом более 90 градусов и прямоугольный треугольник с одним углом 90 градусов.
Что касается треугольников, необходимо знать несколько компонентов, включая площадь и периметр треугольника. Ниже приводится объяснение площади и периметра треугольника вместе с примером проблемы.
Площадь Треугольника

Площадь, площадь или площадь - это величина, которая выражает двумерный размер, а именно часть поверхности, четко обозначенную замкнутой кривой или линией.
Площадь треугольника равна размеру самого треугольника. Ниже приводится формула площади треугольника:
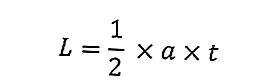
где L - площадь треугольника (см 2 ), a - основание треугольника (см), а h - высота треугольника (см).
Пример площади треугольника.
Пример проблемы 1
Есть острый треугольник с длиной основания a = 10 см и высотой h = 8 см. Вычислите площадь треугольника.
Также прочтите: Животные: характеристики, типы, примеры [ПОЛНОЕ объяснение]Решение:
Если: a = 10 см, h = 8 см
Разыскивается: Площадь треугольника?
Ответ:
L = ½ xaxt
= ½ х 10 х 8
= 40 см2
Итак, площадь острого треугольника 40 см2.
Пример проблемы 2
Прямоугольный треугольник имеет основание 15 см и высоту 20 см. Найдите и вычислите площадь прямоугольного треугольника.
Решение:
Если: a = 15 см, h = 20 см
Разыскивается: Площадь треугольника?
Ответ:
L = ½ xaxt
= ½ х 15 х 20
= 150 см2
Итак, площадь прямоугольного треугольника составляет 150 см2.
Пример проблемы 3
Тупой треугольник с основанием 8 см и высотой 3 см, тогда какова площадь треугольника?
Решение:
Если: a = 8 см, h = 3 см
Разыскивается: Площадь треугольника?
Ответ:
L = ½ xaxt
= ½ х 8 х 3
= 12 см2
Итак, площадь тупого треугольника составляет 12 см2.
Пример задачи 4
Равнобедренный треугольник с такой же длиной стороны составляет 13 см, а основание треугольника - 10 см. Какова площадь равнобедренного треугольника?
Решение:
Вы знаете: s = 13 см, a = 10 см
Разыскивается: Площадь треугольника?
Ответ:
Высота треугольника неизвестна, поэтому мы используем формулу Пифагора, чтобы найти высоту треугольника:

Так как высота треугольника известна, то:
L = ½ xaxt
= ½ х 10 х 12
= 60 см2
Итак, площадь равнобедренного треугольника составляет 60 см2.
Периметр треугольника

Периметр - это количество сторон двумерной формы. Итак, периметр треугольника - это сумма сторон самого треугольника.
Вот формула периметра треугольника:
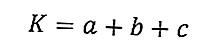
где K - периметр треугольника (см), а a, b, c - длины сторон треугольника (см).
Пример периметра треугольника
Пример проблемы 1
У равностороннего треугольника длина сторон 15 см. Каков периметр треугольника?
Решение:
Вы знаете: длина стороны = 15 см.
Спрашивают: окружность =….?
Ответ:
K = сторона a + сторона b + сторона c
поскольку это равносторонний треугольник, длины трех сторон равны.
К = 15 + 15 + 15
= 45 см
Итак , периметр равностороннего треугольника 45 см.
Также прочтите: Социальное взаимодействие - полное определение и объяснениеПример проблемы 2
У произвольного треугольника стороны 3 см, 5 см и 8 см. Вычислите периметр треугольника.
Решение:
Вы знаете: a = 3 см, b = 5 см и c = 8 см.
Спрашивают: окружность =….?
Ответ:
K = сторона a + сторона b + сторона c
= 3 + 5 + 8
= 16 см
Итак, периметр треугольника равен 16 см.
Пример проблемы 3
Равнобедренный треугольник имеет стороны 10 см и основание 6 см. Вычислите периметр равнобедренного треугольника.
Решение:
Вы знаете: стороны 10 см в длину, а 6 см в длину.
Спрашивают: окружность =….?
Ответ:
K = сторона a + сторона b + сторона c
поскольку треугольник равнобедренный, то есть две стороны одинаковой длины, а именно 10 см, тогда K = 10 + 10 + 6 = 26 см.
Итак, периметр равнобедренного треугольника равен 26 см.
Пример задачи 4
Равнобедренный треугольник имеет высоту 8 см и основание 12 см. Вычислите периметр треугольника.
Решение:
Вы знаете: высота треугольника h = 8 см.
сторона основания a = 12 см
Спросил : окружность =….?
Ответ:
K = сторона a + сторона b + сторона c
Две стороны треугольника неизвестны, поэтому мы используем формулу Пифагора, чтобы найти длину этой стороны.

К = 10 + 10 + 12
К = 32 см
Итак, периметр равнобедренного треугольника равен 32 см.
Это объяснение площади треугольника и периметра треугольника, а также примеры и обсуждение. Может быть полезно.
