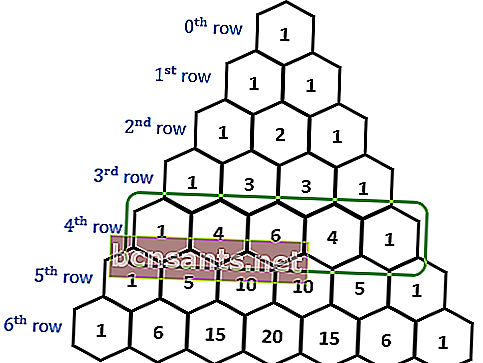
Треугольник Паскаля - это набор треугольников, созданный сложением соседних элементов в предыдущей строке. Такое расположение треугольников получается путем добавления соседних элементов в предыдущем ряду.
Предположим, что переменные a и b складываются вместе, а затем возведены в степень от 0 до степени 3, результатом является следующее описание.
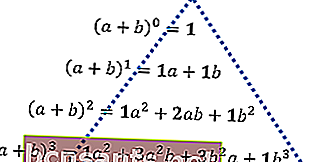
Затем рассмотрите расположение чисел, выделенных жирным шрифтом сверху вниз, пока не найдете треугольную форму. Этот числовой узор в дальнейшем именуется треугольником Паскаля.
Понимание треугольника Паскаля
Треугольник Паскаля - это геометрическое правило биномиального коэффициента в треугольнике.
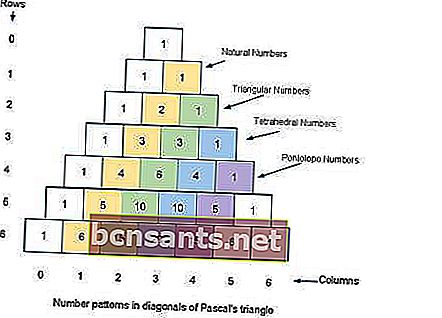
Треугольник назван в честь математика Блеза Паскаля, хотя другие математики изучали его за несколько столетий до него в Индии, Персии, Китае и Италии.
Понятие правил
Концепция треугольника Паскаля - это система расчета этого треугольника независимо от переменных a и b. Это означает, что достаточно обратить внимание на биномиальный коэффициент, а именно:
- В нулевой строке напишите только цифру 1.
- В каждой строке ниже напишите цифру 1 слева и справа.
- Сумма двух чисел выше, записанная в строке ниже.
- 1 слева и справа согласно (2), всегда окружает результат (3)
- Расчеты можно продолжить по той же схеме.
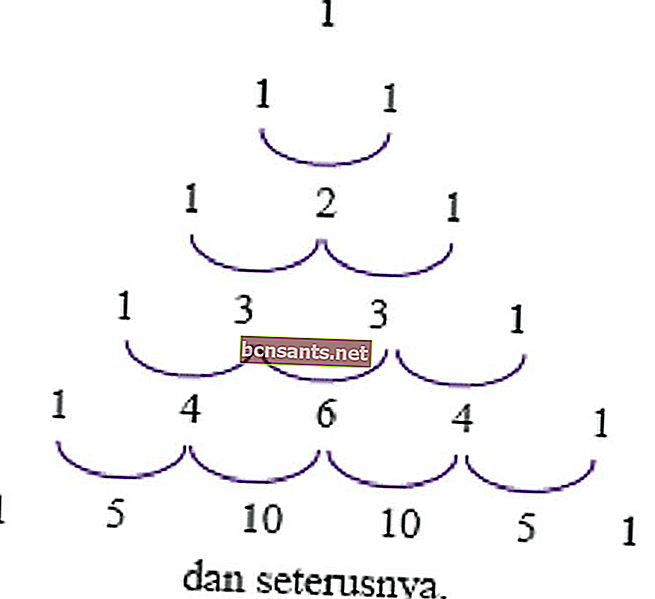

Одно из применений этого треугольника - определить коэффициент мощности (a + b) или (ab), чтобы сделать его более эффективным. Это использование описано в следующих примерах.
Пример проблем
Подсказка: обратите внимание на треугольник Паскаля.
1. Какой перевод (а + б) 4?
Решение : Для (a + b) 4
- Сначала располагаются переменные a и b, начиная с a4b или a4
- Затем степень a падает до 3, что составляет a3b1 (сумма в степени ab должна быть 4).
- Затем сила a падает до 2, превращаясь в a2b2.
- Затем степень a падает до 1, становясь ab3
- Затем степень a падает до 0, до b4
- Затем напишите уравнение с коэффициентом перед пробелом.
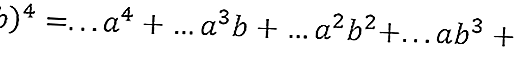
Согласно рисунку 2 в 4-м порядке получаются числа 1,4,6,4,1, так что перевод (a + b) 4 получается

2. Какой коэффициент a3b3 при (a + b) 6?
Также прочтите: Материал магнитного поля: формулы, примеры проблем и объясненияПоселение :
На основании вопроса номер 1 упорядочен порядок переменных из (a + b) 6, а именно
a6, a5b1, a4b2, a 3 b 3 .
Это означает, что на четвертом месте (рисунок 2, последовательность 6) в шаблоне 1, 6, 15, 20 стоит 20 . Таким образом, можно записать 20 a3b3.
3. Определите перевод (3a + 2b) 3
Поселок
Общая формула для треугольника Паскаля как суммы переменных a и b в степени 3 представлена следующим образом

Заменяя переменные на 3a и 2b, получаем

