
Строительство пространства - это тема, которая часто обсуждается в математике, формула часто является математической задачей на уровне начальной и средней школы.
Пространство здания можно интерпретировать как здание, которое математически имеет объем или содержание. Также можно интерпретировать, что форма пространства - это трехмерная форма, которая имеет объем или пространство и ограничена сторонами.
Существуют различные формы самого пространства, такие как блоки, кубы, трубы, шары и так далее.
Каждая из этих форм имеет формулу для объема и площади соответственно. Иногда это затрудняет запоминание многим ученикам.
Далее я составил полный список строительных формул, чтобы вы могли легко решать различные математические задачи по этому предмету.
1. Куб
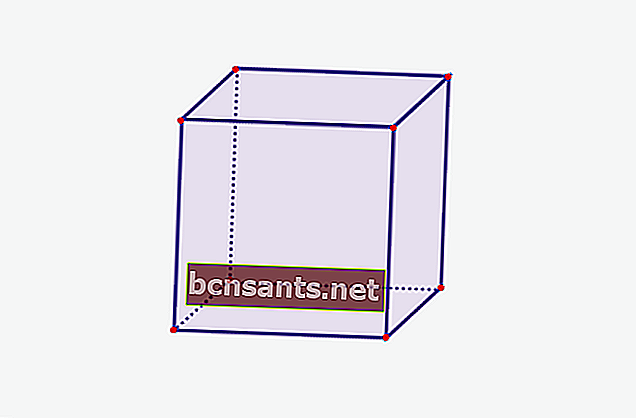
| Объем куба | V = sxsxs |
| Площадь поверхности куба | L = 6 х (sxs) |
| Обведите куб | К = 12 шт. |
| Площадь одной стороны | L = sxs |
2. Балки
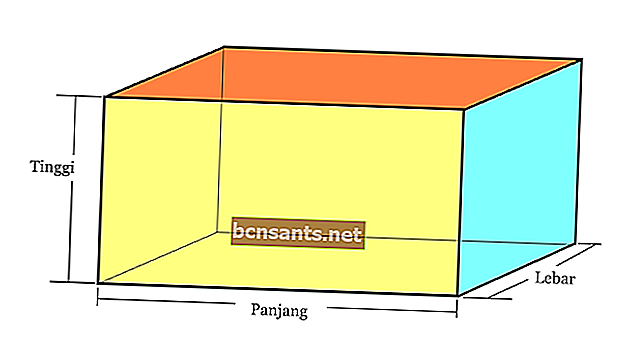
| Объем блока | V = pxlxt |
| Площадь поверхности блока | L = 2 х (pl + lt + pt) |
| Диагональное пространство | d = √ ( p2 + l2 + t2) |
| Окружность балки | К = 4 х (ш + л + в) |
3. Треугольная призма.
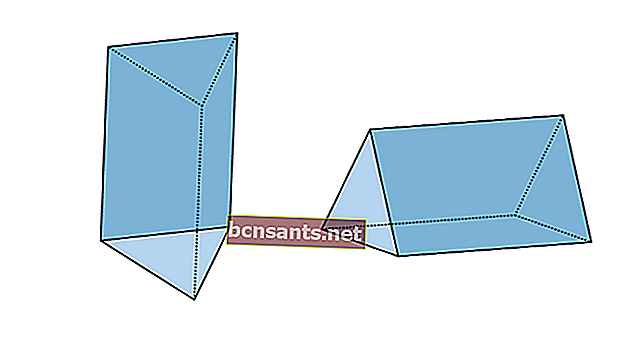
| Объем треугольной призмы | V = площадь основания xt |
| Площадь поверхности треугольной призмы | L = периметр основания xt + 2 x площадь основания треугольника |
4. Пятый четырехугольник
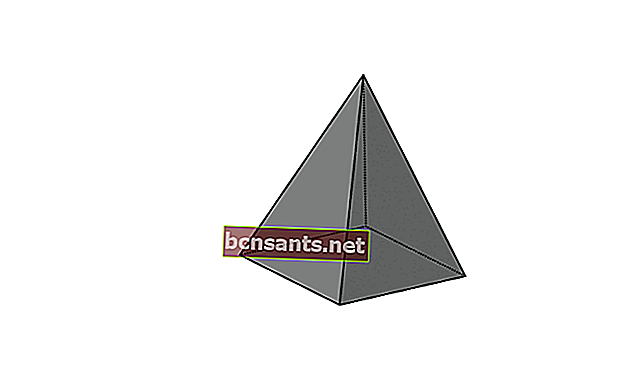
| Объем пирамиды | V = 1/3 xpxlxt |
| Площадь поверхности пирамиды | L = площадь основания + площадь оболочки пирамиды |
5. Пятый треугольник
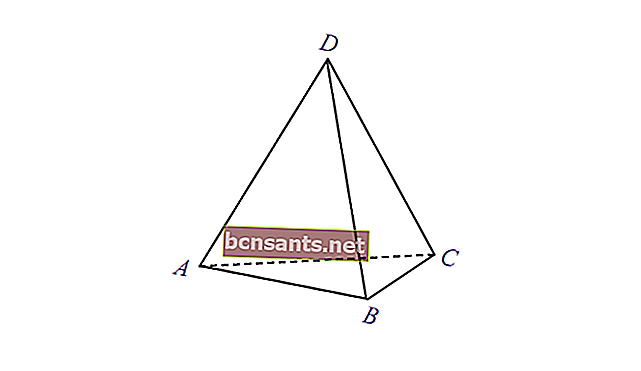
| Объем пирамиды | V = 1/3 x площадь основания xt |
| Площадь поверхности | L = площадь основания + площадь оболочки пирамиды |
6. Трубки

| Объем трубки | V = π x r2 xt |
| Площадь поверхности трубки | L = (2 x площадь основания) + (периметр основания x высота) |
7. Конусы

| Объем конуса | V = 1/3 x π x r2 xt |
| Площадь поверхности конуса | А = (π x r2) + (π xrxs) |
8 мяч

| Объем шара | V = 4/3 х π х r3 |
| Площадь поверхности мяча | А = 4 х π х r2 |
Полная таблица строительных формул
Вы также можете кратко ознакомиться с приведенным выше списком, просмотрев приведенную ниже таблицу. Вы также можете сохранить это изображение, чтобы увидеть его снова в любое время.
Это объяснение формулы строительной формы для расчета объема и площади поверхности.
Надеюсь, приведенное выше объяснение поможет вам понять форму пространства, чтобы вы могли использовать его для решения математических задач и его различных приложений в повседневной жизни.
Справка
- Обзор формул объема - Академия Хана
- Таблица формул геометрии
