
Ожидаемая частотаколичество появлений, ожидаемых в результате многократного проведения экспериментов, которые также известны как экспериментальные испытания.
Или произведение вероятности события, например, события А на количество проведенных экспериментов.
Проще говоря, вы когда-нибудь играли в Людо? Бросить два кубика одновременно и ожидать, что на обоих кубиках выпадет шестерка? Если это так, это означает, что вы применили теорию ожидаемой частоты .
Формулы ожидаемой частоты
В общем, формула ожидаемой частоты выглядит следующим образом:
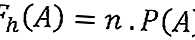
Информация:
F h (A) = ожидаемая частота события A
n = количество вхождений A
P (A) = вероятность события A.
Примеры вопросов с ожидаемой частотой
Пример проблемы 1
- Два кубика бросаются вместе 144 раза. Определите шанс возникновения надежды
- Шесть на обоих умирают.
- Число на обоих кубиках составляет шесть.
Решение:
Чтобы решить такую проблему, сначала подсчитайте общее количество вхождений. Все события обозначаются буквой S, тогда:
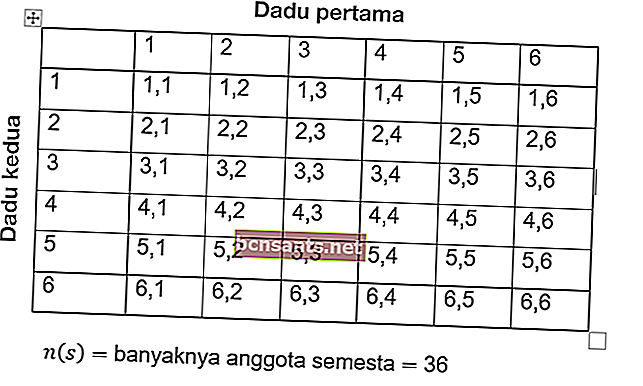
Так что количество членов вселенной чисел равно n (s) = 36.
1. Появление числа шесть на обоих кубиках.
Из двух появившихся чисел только одно - (6,6), тогда:
п (1) = 1
Количество экспериментов было 144 раза, затем
n = 144
Таким образом,
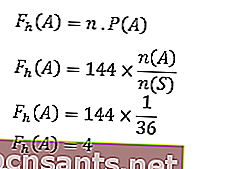
Итак, ожидаемая частота появления числа шесть на обоих кубиках - 4 раза.
2. Появление шести кубиков.
Для общего количества игральных костей шесть, а именно

Количество экспериментов было 144 раза, затем

Таким образом,

Итак, ожидаемая частота выпадения шести игральных костей - 20 раз.
Пример задачи 2
Одна монета, которая была подброшена в воздух 30 раз. Определите ожидаемую частоту появления на числовой стороне.
Также прочтите: Формулы ускорения + примеры проблем и решенийРешение:
Вселенная этого инцидента состоит только из двух, а именно: сторона числа и сторона изображения, или записанная.

тогда n (S) = 2
Количество подброшенных монет 30 раз, тогда n = 30
У числа только одна сторона, поэтому n (A) = 1
Ожидаемая частота событий:
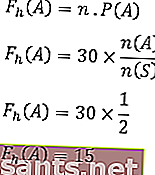
Таким образом, ожидаемая частота появления номера стороны - 20 раз.
Вывод
Таким образом, ожидаемая частота - это частота или количество испытаний, умноженное на вероятность события, в результате которого получится количество ожиданий, возникающих в отношении конкретного события.
Итак, после объяснения выше, можете ли вы рассчитать свои надежды на выигрыш в лотерею? Какие уловки нужно делать, чтобы ваши надежды на победу были высоки?
Напишите свой верный трюк в комментариях и дайте им знать.
Таким образом, объяснение формулы и понимания, а также примеры частоты ожиданий, надеюсь, это будет полезно и до встречи в следующем материале
