
Неопределенный интеграл или также известный как антипроизводная - это форма операции интегрирования, которая создает новую функцию .
Интеграл играет очень важную роль в математике. Теория может определить площадь под кривой функции.
Интеграл полезен для предела суммы, который является непрерывным по непрерывной функции. Интеграл - это противоположное производное. Тогда, если f - непрерывная функция, то интегральный результат функции f обозначается F.
Интегральные типы, основанные на определенных функциональных границах, не определены. Ниже обсуждаются типы интегралов с неопределенными пределами.
Неопределенный интеграл
Неопределенный интеграл, также известный как антипроизводная или анти-диверенциал, - это форма операции интегрирования, которая создает новую функцию.
Рассмотрим следующее уравнение.

с константой C. Неопределенная интегральная формула имеет следующий вид
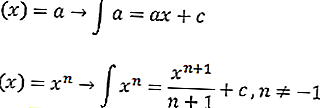
или равно

с участием
- a (x) ^ n = функция уравнения
- a = постоянный
- x = переменная
- n = Степень функции уравнения
- C = постоянная
Результатом этого неопределенного интеграла является функция, которая является новой функцией, которая не имеет определенного или определенного значения, потому что в новой функции все еще есть переменные.
Чтобы лучше понять концепцию неопределенного интеграла, рассмотрим приведенный ниже пример задачи.

На основе этого примера можно сформулировать интегральную операцию, а именно
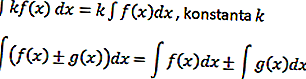
Тригонометрический интеграл
Интеграл функции не обязательно является константой, линейной или полиномиальной. В этом межгалактическом решении часто используются тригонометрические элементы.
В тригономической функции также применяются определения интегралов, приведенные в следующей таблице.
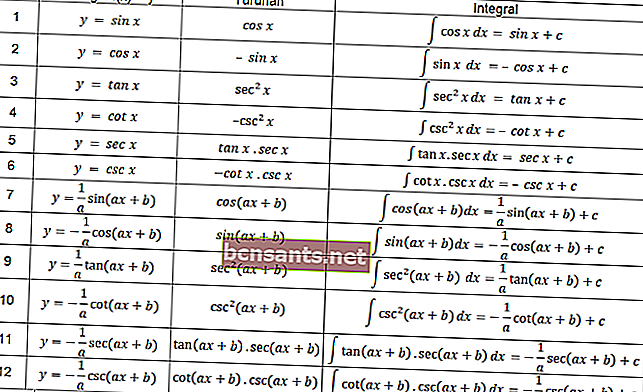
Вы можете использовать уравнения в таблице выше для решения интегральной задачи, связанной с тригонометрией.
Чтобы лучше понять тригонометрические интегралы, вы можете понять следующие примеры.
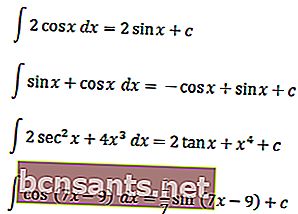
Так объяснялись неопределенные интегралы от обычных и специальных тригонометрических функций. Надеюсь, это можно будет хорошо изучить.
Также прочтите: Нормы приличия: определение, цели, санкции и примеры [FULL]Чтобы лучше понять концепцию этого интеграла, вы можете попрактиковаться в выполнении практических вопросов. Если вы хотите что-то спросить, запишите это в колонку комментариев.
