
Периметр треугольника - это общая длина стороны треугольника. Следовательно, формула для периметра треугольника - K = a + b + c или сумма всех сторон треугольника.
Что это значит, когда вы кружите вокруг треугольного сада? Ага! Вы обводите фигуру треугольника. Что такое плоский треугольник? Ниже приводится объяснение треугольника, типа треугольника и того, как определить или формула для периметра треугольника.
Объяснение треугольника
Треугольник - это форма, образованная тремя пересекающимися линиями, образующими угол. Количество углов в треугольнике - 180 градусов.
Треугольники - это простейшие плоские формы, потому что они являются элементами, образующими другие плоские формы, такие как квадраты, прямоугольники, круги и элементы плоских форм, которые образуют такие формы, как призмы и пирамиды.
Характеристики треугольника
Чтобы еще больше объяснить значение треугольника, я нарисую ниже произвольный треугольник ABC:
Элементы треугольника ABC включают:
- Точки A, B и C называются вершинами.
- Прямые AB, BC и CA называются сторонами треугольника.
- Различные треугольники можно увидеть по сторонам и углам, образованным треугольником.
Типы треугольников
Типы треугольников сильно различаются в зависимости от длины сторон и углов, образующих треугольник. Ниже представлено разделение на типы треугольников.
Типы треугольников по длине сторон
- Равносторонний треугольник
А именно треугольник со всеми тремя сторонами одинаковой длины. Кроме того, три угла, образованные боковым треугольником, имеют одинаковый размер, который составляет 60 градусов, потому что количество углов треугольника составляет 180 градусов.
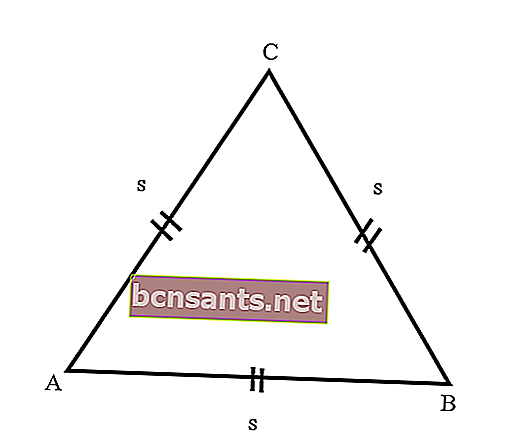
Чтобы узнать больше о равносторонних треугольниках, рассмотрите следующее объяснение свойств равносторонних треугольников:

На рисунках (b) - (d) видно, что форма треугольника ABC может занимать его рамку точно с использованием трех способов, а именно, повернут на 120 градусов с центром в точке O (посмотрите на направление вращения) на (Рисунок b) повернут на 240 градусов в центре вращения. в точке O (на рисунке c), которая повернута на 360 градусов (один полный оборот) в центральной точке в точке O (на рисунке d).
Также прочтите: Формулы возможностей и примеры проблем.В соответствии с пояснениями к фигурам от a до f, равносторонний треугольник ABC имеет симметрию вращения до уровня 3. Между тем, фигуры e, f и g, перевернутые, могут правильно занимать кадр. Для этого треугольник ABC имеет 3 оси симметрии. На картинке выше оси симметрии - CD, BF и AE. Так что равносторонний треугольник может занимать в кадре ровно 6 способов.
Основываясь на некоторых из описаний выше, некоторые из свойств, которые существуют в равностороннем треугольнике, включают в себя: он имеет 3 уровня симметрии вращения, 3 оси симметрии, 3 равносторонние стороны, 3 равных угла по 60 градусов и может занимать рамку максимум 6 способами.
- Равнобедренный треугольник
А именно треугольник с одной стороной одинаковой длины. Равнобедренный треугольник имеет два равных угла, то есть углов, обращенных друг к другу.
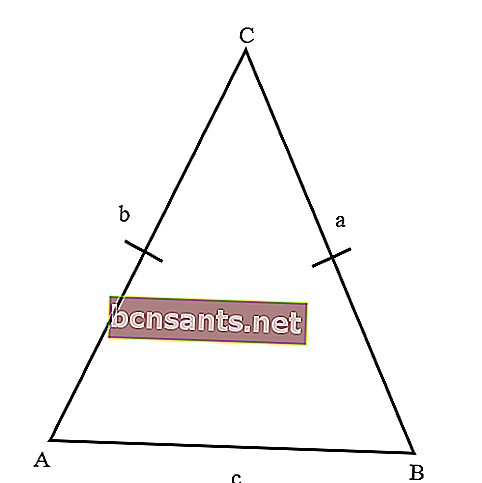
Ниже приведены свойства равнобедренного треугольника;
- Строя равнобедренный треугольник, вращая его на один полный оборот, он занимает рамку ровно в одну сторону. Таким образом, треугольник самакаки имеет вращающуюся симметрию единицы.
- Между тем, у равнобедренного треугольника только одна ось симметрии.
- Любой треугольник
А именно треугольник, у которого все три стороны не одинаковой длины и три угла не равны.

Вот свойства любого треугольника:
- Имеет три стороны разной длины. (На рисунке выше подразумеваются три стороны - это длина BA ≠ CB ≠ AC).
- Не имеет симметрии складок.
- Имеет только одну вращающуюся симметрию.
- Три угла имеют разные размеры.
Виды треугольников по углу
- Острый треугольник
А именно треугольник, все три угла которого образуют острый угол. Острый угол - это угол от 0 до 90 градусов.
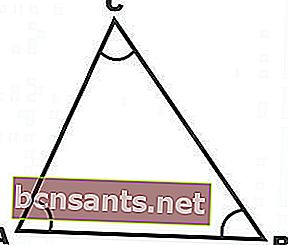
- Тупой треугольник
А именно треугольник с одним углом, образующим тупой угол. Тупой угол - это угол, величина которого находится в диапазоне от 90 до 180 градусов.
Также читайте: Решения для часто забытых формул!
- Прямоугольный треугольник
А именно треугольник, один из углов которого составляет угол 90 градусов.
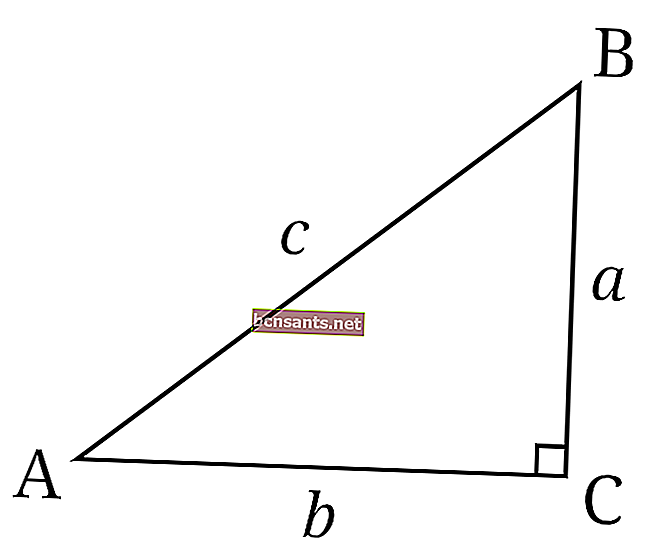
Формула периметра треугольника
Периметр формы получается из количества длин краев (sisis), образующих форму.
Таким образом, формулу для периметра треугольника можно получить, сложив каждую сторону треугольника.
Периметр треугольника = длина 1-й стороны + длина 2-й стороны + длина 3-й стороны
К = а + Ь + с
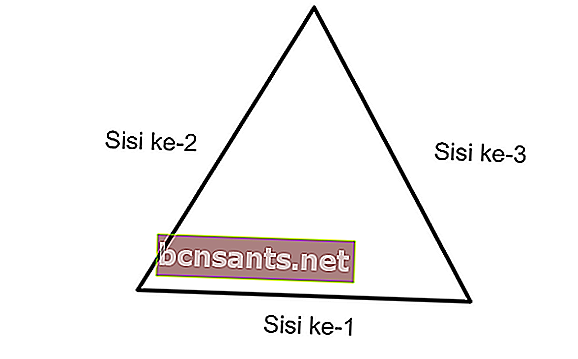
Пример задачи поиска периметра треугольника
Пример проблемы 1.
У равностороннего треугольника длина стороны 3 см, какова его окружность!
Решение:
Вы знаете: s = 3 см
Разыскивается: периметр треугольника?
Ответ:
У равносторонних треугольников одинаковые стороны,
К = s + s + s
К = 3 + 3 + 3
К = 9 см
Итак, периметр равностороннего треугольника равен 9 см.
Пример проблемы 2.
Общая длина стороны равнобедренного треугольника составляет 36 см. Самая длинная сторона - 13 см. Какая длина самой короткой стороны?
Решение:
Вы знаете, что = К = 36 см; б = а = 13 см
Требуется : длина самой короткой стороны?
Ответ :
Периметр треугольника = a + b + c
36 = 13 + 13 + с
c = 10 см
Итак, длина самой короткой стороны треугольника 10 см.
Пример проблемы 3.
Вам дается любой треугольник со сторонами 9, 11, 13 см. Вычислите периметр треугольника!
Решение:
Известно, что : а = 13 см; б = 9 см; c = 11 см
Разыскивается : периметр треугольника?
Ответ:
К = а + Ь + с
К = 13 +9 +11
К = 33 см
Итак, периметр треугольника 33 см.
Пример задачи 4.
Рассчитайте периметр равнобедренного треугольника площадью 12 см2 и длиной стороны 6 см!
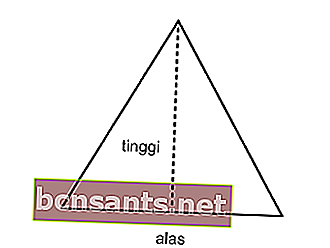
Решение:
Вы знаете: L = 12 см2; а = 6 см
Разыскивается: периметр треугольника?
Ответ:
Чтобы найти периметр треугольника, необходимо знать длину сторон треугольника.
Используйте площадь, чтобы найти высоту треугольника
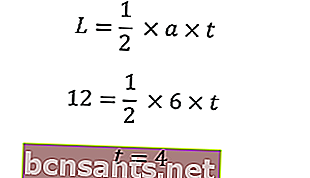
Используя систему Пифагора, мы узнаем гипотенузу равнобедренного треугольника, введя длину основания (a) и высоту треугольника (t).

Используя приведенное выше уравнение, мы получаем гипотенузу треугольника
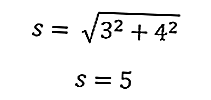
Это позволит сразу рассчитать периметр треугольника.
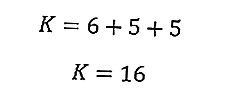
Итак, периметр треугольника равен 16 см.
Ссылка : Треугольник - математика - это весело
