
Формула Пифагора - это формула, используемая для определения длины одной из сторон треугольника.
Формула Пифагора, также известная как теорема Пифагора, является одним из первых преподаваемых предметов математики.
С начальной школы нас учили этой формуле Пифагора.
В этой статье я еще раз вернусь к утверждению теоремы Пифагора вместе с примерами проблем и их решений.
История Пифагора - Пифагор
На самом деле Пифагор - это имя человека из древнегреческих времен 570 - 495 гг. До н.э.
Пифагор был блестящим философом и математиком своего времени. Об этом свидетельствуют его открытия, которые позволили решить проблему длины стороны треугольника с помощью очень простой формулы.
Теорема Пифагора
Теорема Пифагора - это математическое утверждение о прямоугольных треугольниках, которое показывает, что длина основания квадрата плюс длина высоты квадрата равняется длине гипотенузы квадрата.
Предположим….
- Длина основания треугольника равна
- Длина высоты b
- Длина гипотенузы c
Таким образом, используя аргумент Пифагора, можно сформулировать отношения между тремя
а 2 + Ь 2 = с 2
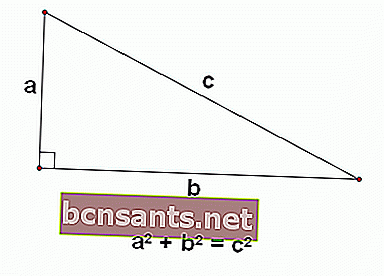
Доказательство теоремы Пифагора.
Если вы наблюдательны, вы сможете представить, что в основном формула Пифагора показывает, что площадь квадрата со стороной a плюс площадь квадрата со стороной b равна площади квадрата со стороной c.
Вы можете увидеть иллюстрацию на следующем изображении:

Вы также можете посмотреть его в следующем видео
Как пользоваться формулой Пифагора
Формула фитагора a 2 + b 2 = c 2 в основном может быть выражена в нескольких формах, а именно:
а2 + Ь2 = с2
с2 = а 2 + Ь 2
а2 = с2 - Ь 2
b2 = c2 -а2
Чтобы решить каждую из этих формул, вы можете использовать значение корня формулы Пифагора, приведенной выше.
Также прочтите: Микроскоп: объяснение, его составные части и функции.
Важное примечание: не забывайте, что приведенные выше формулы применимы только к прямоугольным треугольникам. Если нет, то не действует.
Тройной Пифагор (Числовой образец)
Тройка Пифагора - это имя шаблона чисел abc, который соответствует формуле Пифагора, приведенной выше.
Эти тройные пифагоры заполняют так много чисел, даже до очень больших чисел.
Вот некоторые примеры:
- 3–4–5
- 5–12–13
- 6–8–10
- 7–24–25
- 8–15–17
- 9–12–15
- 10–24–26
- 12–16–20
- 14 - 48 - 50
- 15–20–25
- 15 - 36 - 39
- 16–30–34
- 17 - 144 - 145
- 19 - 180 - 181
- 20–21–29
- 20 - 99 - 101
- 21 - 220 - 221
- 23 - 264 - 265
- 24 –143 - 145
- 25 - 312 - 313
- так далее
Список можно продолжить до очень большого числа.
По сути, числа будут совпадать, если вы подставите значения в формулу a 2 + b 2 = c 2
Примеры полных вопросов и обсуждения
Чтобы лучше понять суть этой формулы Пифагора, давайте рассмотрим пример полной проблемы и последующее обсуждение.
Пример пифагорейской формулы 1
1. У треугольника длина стороны BC 6 см и стороны AC 8 см. Сколько см гипотенуза треугольника (AB)?
Решение:
Известный :
- BC = 6 см
- AC = 8 см
Требуется длина AB?
Ответ:
AB2 = BC2 + AC2
= 62 + 82
= 36 + 64
= 100
AB = √100
= 10
Таким образом, длина стороны АВ (наклонной) составляет 10 см.
Пример теоремы Пифагора 2
2. Известно, что треугольник имеет гипотенузу длиной 25 см , а вертикальная сторона треугольника имеет длину 20 см . Какова длина плоской стороны?
Решение:
Известно: мы приводим пример, чтобы было проще
- c = гипотенуза, b = плоская сторона, a = вертикальная сторона
- c = 25 см, a = 20 см
Требуется: Длина плоской стороны (б)?
Ответ:
б2 = с2 - а2
= 252–202
= 625–400
= 225
б = √225
= 15 см
Так, чтобы длина плоской стороны треугольника была 15 см .
Пример формулы Пифагора 3
3. Какова длина вертикальной стороны треугольника, если известно, что гипотенуза треугольника составляет 20 см , а плоская сторона имеет длину 16 см .
Поселение :
Известно: сначала делаем пример и значение
- c = гипотенуза, b = плоская сторона, a = вертикальная сторона
- c = 20 см , b = 16 см
Требуется: Длина по вертикали (а)?
Ответ:
а2 = с2 - Ь2
= 202–162
= 400–256
= 144
а = √144
= 12 см
Отсюда получаем, что длина вертикальной стороны треугольника составляет 12 см .
Пример тройной задачи Пифагора 4
Продолжите значение следующей тройки Пифагора….
3, 4,….
6, 8,….
5, 12,….
Решение:
Подобно решениям в предыдущих задачах, это тройное пифагорово соотношение может быть решено с помощью формулы c2 = a 2 + b 2.
Попробуйте сами рассчитать….
Ответ (подлежащий сопоставлению):
- 5
- 10
- 13
Пример формулы Пифагора Задача 5
Учитывая, что три города (A, B, C) образуют треугольник, локти которого находятся в городе B.
Расстояние до города AB = 6 км, расстояние до города BC = 8 км, какое расстояние до города AC?
Решение:
Вы можете использовать формулу теоремы Пифагора и получить результат расчета расстояния до города AC = 10 км.
Таким образом, обсуждение формулы Пифагора - аргументы теоремы Пифагора, которые изложены просто. Надеюсь, вы сможете хорошо это понять, чтобы позже вы могли понять другие математические темы, такие как тригонометрия, логарифмы и т. Д.
Если у вас остались вопросы, вы можете задать их прямо в колонке комментариев.
Справка
- Что предлагает Пифагор? - спрашивающий сын
- Теорема Пифагора - математика - это весело
