
Квадратичное уравнение - это одно из математических уравнений переменной, имеющее наивысшую степень двойки.
Общая форма квадратного уравнения или ПК выглядит следующим образом:
ах 2 + Ьх + с = 0
где x - переменная, a , b - коэффициент, c - постоянная. Значение a не равно нулю.
Формы графиков
Если квадратное уравнение описывается в декартовых координатах (x, y), то оно образует параболический граф. Поэтому квадратные уравнения также часто называют параболическими уравнениями .
Ниже приводится пример формы этого уравнения в виде параболического графика.
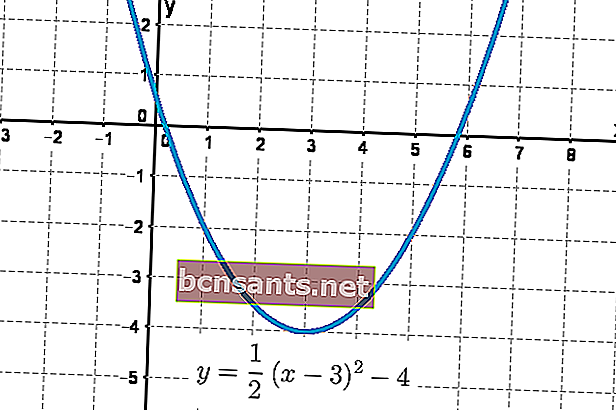
В общем уравнении значения a , b и c сильно влияют на результирующий параболический рисунок.
Значение a определяет вогнутую или выпуклую кривую параболы. Если значение a> 0, то парабола откроется (вогнется) . И наоборот, если a <0 , то парабола развернется вниз (выпуклая) .

Значение b в уравнении определяет вершину параболы . Другими словами, определить значение оси симметрии кривой, равное x = - b / 2a .

Постоянное значение c на графике уравнения определяет точку пересечения параболической функции на оси ординат . Ниже приведен параболический график с изменениями постоянного значения c .

Корни квадратного уравнения (ПК)
Решение квадратного уравнения называется кар-корнем квадратного уравнения .
Различные корни PK
Типы корней PK можно легко найти, используя общую формулу D = b2 - 4ac из общего уравнения для квадратичного ax2 + bx + c = 0.
Ниже приведены виды корней квадратных уравнений.
1. Настоящий корень (D> 0)
Если значение D> 0 от ПК, это приведет к получению реальных корней уравнения, но с разными корнями. Другими словами, x1 не то же самое, что x2.
Пример уравнения с вещественным корнем (D> 0)
Найдите корневой тип уравнения x2 + 4x + 2 = 0.
Решение:
а = 1; b = 4; и c = 2
D = b2 - 4ac
D = 42 - 4 (1) (2)
D = 16 - 8
D = 8
Итак, поскольку значение D> 0, то корень имеет тип real root.
2. Вещественный корень равен x1 = x2 (D = 0).
Тип корня квадратного уравнения, который дает корни с одинаковым значением (x1 = x2).
Пример действительных корней (D = 0)
Найдите значение корня PK 2x2 + 4x + 2 = 0.
Также читайте: Типы круговоротов в воде (+ полное изображение и объяснение)Решение:
а = 2; b = 4; с = 2
D = b2 - 4ac
D = 42 - 4 (2) (2)
D = 16 - 16
D = 0
Итак, поскольку значение D = 0, доказано, что корни настоящие и двойниковые.
3. Мнимые корни / ненастоящие (D <0)
Если значение D <0, то корень квадратного уравнения будет мнимым / не действительным.
Пример мнимых корней (D <0) /
Найдите корневой тип уравнения x2 + 2x + 4 = 0.
Решение:
а = 1; b = 2; с = 4
D = b2 - 4ac
D = 22 - 4 (1) (4)
D = 4 - 16
D = -12
Итак, поскольку значение D <0, корень уравнения является нереальным или мнимым корнем.
Найдите корни квадратного уравнения
Есть несколько методов, которые можно использовать для поиска корней квадратного уравнения. Среди них факторизация, полные квадраты и использование формулы abc.
Ниже описаны несколько методов поиска корней уравнения.
1. Факторизация
Факторизация / факторинг - это метод нахождения корней путем поиска значения, которое, если умножить, даст другое значение.
Есть три формы квадратных уравнений (ПК) с разной факторизацией корня, а именно:
| Нет. | Форма уравнения | Корневая факторизация |
| 1 | х 2 + 2кси + у 2 = 0 | (х + у) 2 = 0 |
| 2 | х 2 - 2кси + у 2 = 0 | (х - у) 2 = 0 |
| 3 | х 2 - у 2 = 0 | (х + у) (х - у) = 0 |
Ниже приводится пример задачи об использовании метода факторизации в квадратных уравнениях.
Решите квадратное уравнение 5x 2 + 13x + 6 = 0, используя метод факторизации.
Решение:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5х (х + 2) + 3 (х + 2) = 0
(5x + 3) (x + 2) = 0
5x = -3 или x = -2
Итак, решение x = -3/5 или x = -2
2. Идеальные квадраты
Идеально квадратичная форма является квадратным уравнением , что дает рациональные числа .
Результаты идеального квадратного уравнения обычно используют следующую формулу:
(x + p) 2 = x2 + 2px + p2
Общее решение совершенного квадратного уравнения выглядит следующим образом:
(x + p) 2 = x2 + 2px + p2
с (x + p) 2 = q, тогда:
(х + р) 2 = д
х + р = ± q
х = -р ± д
Ниже приведен пример проблемы использования метода идеального уравнения.
Решите уравнение x2 + 6x + 5 = 0 с помощью метода идеальных квадратных уравнений!
Решение:
х2 + 6х +5 = 0
х2 + 6х = -5
Следующим шагом будет сложение одного числа с правой и левой стороны, чтобы получился идеальный квадрат.
х2 + 6х + 9 = -5 + 9
х2 + 6х + 9 = 4
(х + 3) 2 = 4
(х + 3) = √4
х = 3 ± 2
Итак, окончательный результат: x = -1 или x = -5.
Также читайте: Определение и различие омонимов, омофонов и омографов3. Квадратичные формулы ABC.
Формула abc является альтернативным выбором, когда квадратное уравнение не может быть решено с помощью факторизации или совершенных квадратичных методов.
Ниже приводится формула abc для квадратного уравнения ax2 + bx + c = 0.
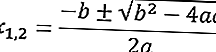
Ниже приведен пример решения задачи квадратного уравнения с использованием формулы abc .
Решите уравнение x2 + 4x - 12 = 0, используя метод формулы abc!
Решение:
х2 + 4х - 12 = 0
где a = 1, b = 4, c = -12

Построение нового квадратного уравнения
Если раньше мы научились находить корни уравнения, то теперь мы научимся составлять квадратное уравнение из корней, которые были ранее известны.
Вот несколько способов создать новый ПК.
1. Постройте уравнения, когда известны корни.
Если уравнение имеет корни x1 и x2, то уравнение для этих корней может быть выражено через
(х- х 1 ) (х- х 2 ) = 0
Пример:
Найдите квадратное уравнение с корнями от -2 до 3.
Решение:
х 1 = -2 и х 2 = 3
(х - (- 2)) (х-3) = 0
(х + 2) (х + 3)
х2-3х + 2х-6 = 0
х2-х-6 = 0
Итак, результатом уравнения для этих корней будет x2-x-6 = 0
2. Постройте квадратное уравнение, если вы знаете количество и произведение корней.
Если корни квадратного уравнения с числом и временами x1 и x2 известны, квадратное уравнение можно преобразовать в следующую форму.
х2- (х 1+ х 2 ) х + (х 1. х 2 ) = 0
Пример:
Найдите квадратное уравнение с корнями 3 и 1/2.
Решение:
х 1 = 3 и х 2 = -1/2
х 1+ х 2 = 3 -1/2 = 6/2 - 1/2 = 5/2
х 1. х 2 = 3 (-1/2) = -3/2
Таким образом, квадратное уравнение:
х2- (х 1+ х 2 ) х + (х 1. х 2 ) = 0
x2– 5/2 x - 3/2 = 0 (каждая сторона умножается на 2)
2x2-5x-3 = 0
Итак, квадратное уравнение для корней 3 и 1/2 равно 2x2-5x-3 = 0.
