
Композиционная функция - это комбинация двух типов функций f (x) и g (x), позволяющая создать новую функцию.
Формулы функции композиции
Символ работы функции композиции - это «о», тогда это может быть композиция или круг. Эта новая функция может быть образована из f (x) и g (x), а именно:
- (туман) (x), что означает, что g входит в f
- (gof) (x), что означает, что f помещается в g
В композиции функция также известна как отдельная функция.
Что такое отдельная функция?
Отдельная функция - это функция, которая может быть обозначена буквами «туман» или может читаться как «f roundabout g». Функция «туман» - это функция g, которая выполняется первой, затем следует f.
Между тем, функция gof считывает функцию g roundabout f. Таким образом, «gof» - это функция, в которой сначала выполняется f, а не g.
Тогда функция (fog) (x) = f (g (x)) → функция g (x) составляется как функция f (x)
Чтобы понять эту функцию, рассмотрите изображение ниже:
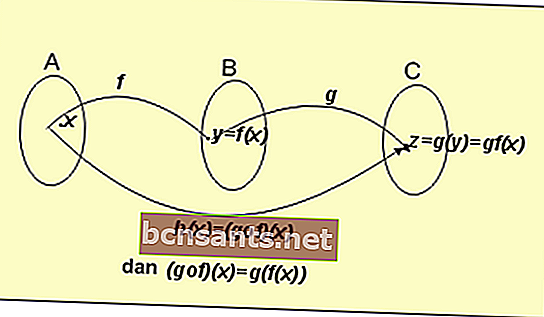
Из приведенной выше схемы формул мы получили следующее определение:
Если f: A → B определяется формулой y = f (x)
Если g: B → C определяется формулой y = g (x)
Тогда мы получаем результат функций g и f:
h (x) = (gof) (x) = g (f (x))
Из приведенного выше определения можно сделать вывод, что функции, включающие функции f и g, можно записать:
- (гоф) (х) = г (е (х))
- (туман) (x) = f (g (x))
Свойства функции композиции
У функции композиции есть несколько свойств, которые описаны ниже.
Если f: A → B, g: B → C, h: C → D, то:
- (туман) (х) ≠ (гоф) (х). Коммутативный характер не применяется
- [fo (goh) (x)] = [(туман) oh (x)]. ассоциативный
- Если тождественная функция - это I (x), то (fol) (x) = (lof) (x) = f (x)
Пример проблем
Проблема 1
Даны две функции, каждая f (x) и g (x), соответственно, а именно:
е (х) = 3х + 2
г (х) = 2 - х
Определите:
а) ( ф о г ) (х)
б) ( г о ж ) (х)
Ответ
Известный:
е (х) = 3х + 2
г (х) = 2 - х
( ф о г ) (х)
"Подключите g (x) к f (x)"
быть:
( ж о г ) (х) = е ( г (х))
= f (2 - х)
= 3 (2 - х) + 2
= 6 - 3x + 2
= - 3x + 8
( г о ж ) (х)
"Подключите f (x) к g (x)"
Пока не станет:
( ж о г ) (х) = г ( е (х))
= г (3x + 2)
= 2 - (3x + 2)
= 2 - 3x - 2
= - 3x
Проблема 2
Если известно, что f (x) = 3x + 4 и g (x) = 3x, каково значение (fog) (2).
Ответ:
(туман) (x) = f (g (x))
= 3 (3х) + 4
= 9x + 4
(туман) (2) = 9 (2) + 4
= 22
Проблема 3
Дана функция f (x) = 3x - 1 и g (x) = 2 × 2 + 3. Значение композиции функции ( g o f ) (1) =….?
Ответ
Известный:
f (x) = 3x - 1 и g (x) = 2 × 2 + 3
( g o f ) (1) =…?
Вставьте f (x) в g (x), затем заполните 1
( g o f ) (x) = 2 (3 x - 1) 2 + 3
( g o f ) (x) = 2 (9 x 2 - 6x + 1) + 3
( g o f ) (x) = 18x 2 - 12x + 2 + 3
( g o f ) (x) = 18 × 2 - 12x + 5
( g o f ) (1) = 18 (1) 2 - 12 (1) + 5 = 11
Проблема 4
Ему даны две функции:
f (x) = 2x - 3
г (х) = х2 + 2х + 3
Если (туман) (а) равно 33, найдите значение 5а.
Ответ:
Искать сначала (туман) (x)
(туман) (x) равно 2 (x2 + 2x + 3) - 3
(туман) (x) равно 2 × 2 4x + 6-3
(туман) (x) равно 2 × 2 4x + 3
33 то же самое, что 2a2 4a + 3
2a2 4a - 30 равно 0
a2 + 2a - 15 равно 0
Также прочтите: Бизнес-формулы: объяснение материала, примеры вопросов и обсуждениеФактор:
(a + 5) (a - 3) равно 0
a = - 5 или равно 3
Чтобы
5a = 5 (−5) = −25 или 5a = 5 (3) = 15
Проблема 5
Если (туман) (x) = x² + 3x + 4 и g (x) = 4x - 5. Каково значение f (3)?
Ответ:
(туман) (x) равно x² + 3x + 4
f (g (x)) равно x² + 3x + 4
g (x) равно 3 Итак,
4x - 5 равно 3
4x равно 8
x равно 2
f (g (x)) = x² + 3x + 4 и для g (x), равного 3, получаем x равным 2
Пока: f (3) = 2² + 3. 2 + 4 = 4 + 6 + 4 = 14
Таким образом, объяснение формулы функции композиции является примером проблемы. Может быть полезно.
