
Абсолютное значение в исчислении очень полезно для решения различных математических задач, как в уравнениях, так и в неравенствах. Ниже приводится полное объяснение абсолютных значений и примеры вопросов.
Определение абсолютной ценности
Все числа имеют соответствующие абсолютные значения. Все абсолютные числа положительны, поэтому абсолютные числовые значения чисел с одним и тем же числом, но с разницей между положительным (+) и отрицательным (-) обозначениями, будут иметь тот же результат абсолютного числа.
Если x является членом действительного числа, то абсолютное значение записывается как | x | и определяется следующим образом:

«Абсолютное значение - это число с одинаковым значением длины или расстояния от начала координат или нулевой точки в координатах».
Можно интерпретировать, что абсолютное значение 5 - это длина или расстояние от точки 0 до точки 5 или (-5).
Абсолютные значения (-9) и 9 равны 9. Абсолютные значения 0 равны 0 и так далее. Нилаа
Я полностью это пойму, посмотрев на следующую картинку:

На картинке выше можно понять, что значение | 5 | расстояние точки 5 от числа 0, а именно 5, и | -5 | расстояние точки (-5) от числа 0 равно 5.
Если | x | представляет расстояние от точки x до 0, тогда | xa | расстояние от точки x до точки a. Например, при выражении расстояния от точки 5 до точки 2 это может быть записано как | 5-2 | = 3

В общем, можно утверждать, что расстояние x до a можно записать с помощью обозначения | xa | или | топор |
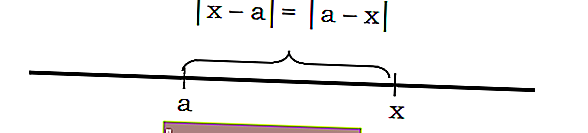
Например, расстояние от числа до точки 3 равно 7:
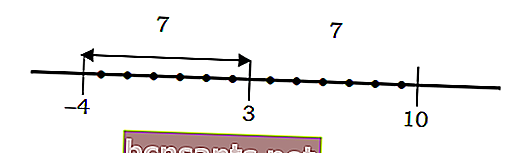
Если описывается в алгебраическом уравнении | x-3 | = 7, его можно решить следующим образом:
Читайте также: Измерение землетрясений с помощью логарифмов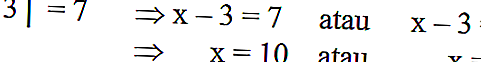
Помните, что | x-3 | - это расстояние от числа x до точки 3, где | x-3 | = 7 - расстояние от числа x до точки 3 вдоль 7 единиц.
Свойства абсолютного значения
В операциях с абсолютными числовыми уравнениями есть свойства абсолютных чисел, которые могут помочь решить абсолютные числовые уравнения.
Ниже приведены свойства абсолютных чисел в целом в уравнениях абсолютных значений:

Свойства модуля неравенства:
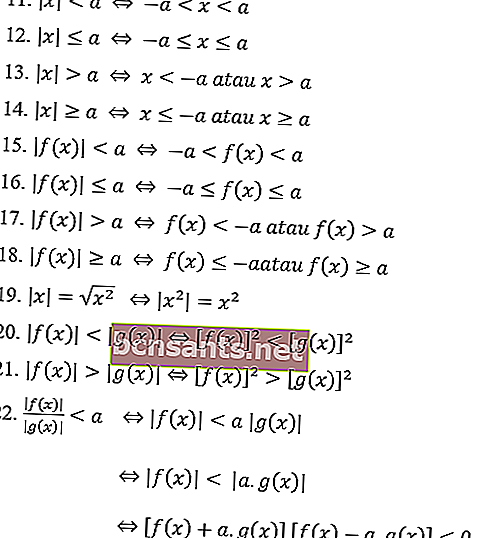
Примеры задач с уравнениями абсолютных значений
Пример проблемы 1
Каково абсолютное значение уравнения | 10-3 |?
Ответ:
| 10-3 | = | 7 | = 7
Пример проблемы 2
Каков результат x для уравнения для абсолютного значения | x-6 | = 10?
Ответ:
Чтобы решить это уравнение, есть два возможных результата для абсолютных чисел
| х-6 | = 10
Первое решение:
х-6 = 10
х = 16
второе решение:
х - 6 = -10
х = -4
Итак, ответ на это уравнение - 16 или (-4)
Пример проблемы 3
Решите и вычислите значение x в следующем уравнении
–3 | x - 7 | + 2 = –13
Ответ:
–3 | x - 7 | + 2 = –13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| х - 7 | = –15 / –3
| х - 7 | = 5
Готово до решения выше, тогда значение x имеет два значения
х - 7 = 5
х = 12
или
х - 7 = - 5
х = 2
поэтому окончательное значение x равно 12 или 2
Пример задачи 4
Решите следующее уравнение и определите значение x
| 7 - 2x | - 11 = 14
Ответ:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
После завершения приведенного выше уравнения числа для абсолютного значения x будут следующими:
7 - 2x = 25
2x = - 18
х = - 9
или
7 - 2x = - 25
2x = 32
х = 16
Таким образом, окончательное значение x равно (- 9) или 16
Пример проблемы 5
Найдите решение следующего уравнения абсолютного значения:
| 4х - 2 | = | x + 7 |
Ответ:
Чтобы решить указанное выше уравнение, используйте два возможных решения, а именно:
Читайте также: Ошибки при чтении результатов опроса об избрании кандидатов.4х - 2 = х + 7
х = 3
или
4х - 2 = - (х + 7)
х = - 1
Итак, решение уравнения | 4x - 2 | = | x + 7 | это x = 3 или x = - 1
Пример задачи 6
Найдите решение следующего уравнения абсолютного значения:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
Какое значение x?
Ответ:
Упрощение: | 3x + 2 | = p
тогда
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(р + 2) (р - 1) = 0
р + 2 = 0
p = - 2 (абсолютное значение не отрицательное)
или
р - 1 = 0
р = 1
| 3x + 2 | = 1
До решения, приведенного выше, есть 2 возможных ответа для x, а именно:
3х + 2 = 1
3x = 1-2
3x = - 1
х = - 1/3
или
- (3x + 2) = 1
3x + 2 = - 1
3x = - 1 - 2
3x = - 3
х = - 1
Таким образом, решение уравнения: x = - 1/3 или x = - 1.
Ссылка: Абсолютное значение - математика - это весело
